Множества
Множества
Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:
- Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.
- Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).
Множества обычно обозначаются заглавными латинскими буквами. Если элемент 
![]() , то это обозначается:
, то это обозначается:
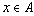
Если каждый элемент множества 
![]() , то говорят, что множество
, то говорят, что множество  подмножеством множества
подмножеством множества 
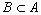
Подмножество 
![]() называется собственным подмножеством, если
называется собственным подмножеством, если
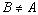
Используя понятие множества можно построить более сложные и содержательные объекты.
