Обычно отношение порядка обозначают знаком
Определение 9
. Отношение


называется
отношением порядка, если оно обладает следующими свойствами:
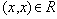
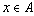 (рефлексивность)
(рефлексивность)
- Если
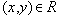
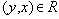 , то
, то 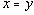
- Если
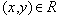
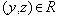 , то
, то 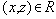
Обычно отношение порядка обозначают знаком


и

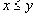
, то говорят, что


. Как и для отношения эквивалентности, условия 1-3 в таких обозначениях выглядят более естественно:
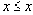
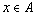 (рефлексивность)
(рефлексивность)
- Если
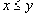
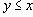 , то
, то 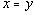
- Если
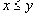
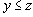 , то
, то 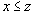
Определение 9
. Пусть отношение 
 , отношение
, отношение 
 , а
, а 
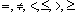 и т.д.). Тогда
и т.д.). Тогда  соединением отношения
соединением отношения 
 с отношением
с отношением 
 называют отношение
называют отношение
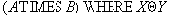 Это частный случай операции общего соединения.
Иногда, для операции
Это частный случай операции общего соединения.
Иногда, для операции 
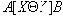
Определение 9
. Отношение
 5НФ
5НФ, если в отношении найдется нетривиальная зависимость соединения.
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении

(i) Отношение

(ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении

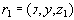
,
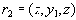
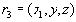
, то отсюда следует, что в отношении

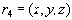
.
Утверждение. Докажем, что при наличии ограничений (i) и (ii), отношение находится в 4НФ, но не в 5НФ.
Доказательство. Покажем, что отношение

Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является
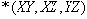

,


не совпадает с множеством всех атрибутов отношения

Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции
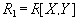
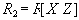
и
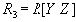

(именно здесь содержится ключевая тонкость, обычно пропускаемая при анализе конкретного состояния отношения

Как и в предыдущих доказательствах, нужно доказать, что
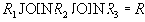

.
Включение
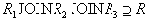

.
Докажем включение
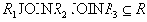
Пусть кортеж
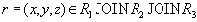
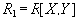
содержится кортеж
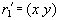
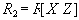
содержится кортеж
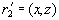
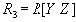
содержится кортеж
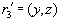

,


атрибутов


и


содержит кортежи
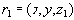
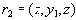
и
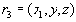

содержится также и кортеж
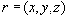 Утверждение доказано
Утверждение доказано.

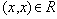
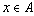 (рефлексивность)
(рефлексивность)
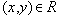
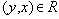 , то
, то 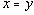
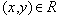
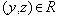 , то
, то 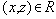



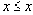
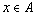 (рефлексивность)
(рефлексивность)
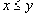
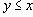 , то
, то 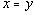
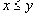
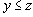 , то
, то 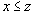



 соединением отношения
соединением отношения 

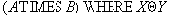 Это частный случай операции общего соединения.
Иногда, для операции
Это частный случай операции общего соединения.
Иногда, для операции 
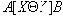

 5НФ, если в отношении найдется нетривиальная зависимость соединения.
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении
5НФ, если в отношении найдется нетривиальная зависимость соединения.
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении  (i) Отношение
(i) Отношение  (ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении
(ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении 
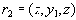

 Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является
Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является 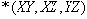

 Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции
Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции 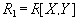
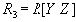
 Как и в предыдущих доказательствах, нужно доказать, что
Как и в предыдущих доказательствах, нужно доказать, что 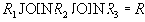
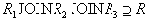
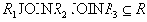 Пусть кортеж
Пусть кортеж 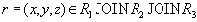
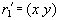
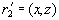
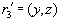



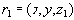
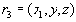
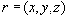 Утверждение доказано.
Утверждение доказано.